Geoffrey West Scale Blue Whale 11000 Calories
Scale by Geoffrey West: A brief summary
Insights into the universal scaling laws that underlie organisms, cities, economies, and companies

Why can we live for up to 120 years but not longer? Why do mice only live 2–3 years but elephants up to 75? Why do we stop growing once we reach maturity? Is there a maximum or optimum size of cities? And why do companies die but cities don't? These are some of the mysteries that Geoffrey West elucidates in his 2017 book "Scale: The Universal Laws of Growth, Innovation, Sustainability, and the Pace of Life in Organisms, Cities, Economies, and Companies".
Scaling of organisms
Scaling refers to how a system responds when its size changes. Research has abundantly demonstrated the predominance of quarter-power scaling laws in biology. For instance, when an animal doubles in size (i.e. doubles its body weight), then its number of cells also roughly doubles, but its metabolic rate only increases by about 75%, rather than 100%, as you would naively expect. This is a phenomenon known as Kleiber's Law, after Max Kleiber who pioneered this type of work in the 1930s. It can be formally written as q₀ ~ M^(¾), whereby q₀ is the animal's metabolic rate, and M the animal's mass. This means that a cat that is 100 times heavier than a mouse only consumes about 100^(¾) ~ 32 times the energy that the mouse consumes. In physics, this nonlinear behavior characterized by the systematic savings as size increases is referred to as sublinear scaling or economy of scale. The figure below, showing metabolic rate as a function of body mass (plotted logarithmically), highlights this behavior.
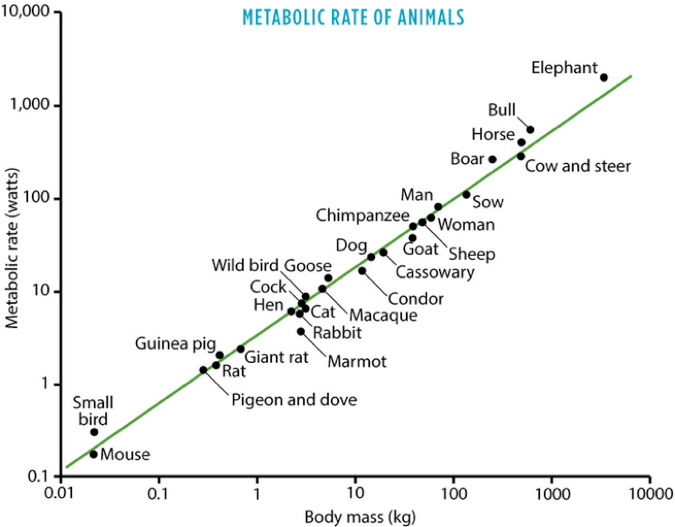
In biology, particularly in animals of the same taxonomic group (such as mammals), these quarter-power scaling laws appear to be universal despite the amazing diversity and complexity of different organisms. We have already seen that metabolic rate scales with an exponent of 3/4. However, myriad other biological variables have been shown to scale as multiples of 1/4, such as life span and length of aortas (exponent of 1/4), and growth rate and heart rate (exponent of -1/4). Taking heart rate, for instance, an exponent of -1/4 means that the heart rate decreases by 25% upon each doubling of the organism. Interestingly, all mammals seem to have the same number of heartbeats over their lifetime — approximately 1.5 billion. Thus, the smallest mammal, the shrew, with a lifespan of only 2–3 years, has an extraordinarily fast heart rate of over 1,000 beats per minute, whereas the blue whale's heart only beats 4–8 times per minute.
Humans have deviated from this number — our heart beats approximately 2.5 billion times over our lifetime — due to our departure from a purely biological life to a predominantly social one, which has extended our lifespan by a factor of two compared to 150 years ago, when the average lifespan was about 35–40 years. This extension was mainly achieved due to the decrease in infant mortality, which arose concomitantly with breakthroughs in medicine, the introduction of indoor plumbing, sanitation, and a generally healthier and cleaner way of living. This has also led to our average daily energy expense to increase from a purely biological 90 watts per person (shown in the figure above), based on 2,000 food calories, to 3,000 watts (in the US it's 11,000 watts!) due to increased energy needs such as housing, lighting, heating, cars, roads, and computers.
The reason why there are no bigger mammals than blue whales and no smaller ones than shrews is also embedded within the constraints of these allometric scaling laws. Our heart pumps blood into the aorta, which then undergoes several rounds of branching into smaller vessels, eventually leading to the terminal units, our capillaries, where oxygen is exchanged with cells. The size of these terminal units is invariant across all mammals, meaning that the capillaries of a shrew are the same size as the ones of a blue whale. However, as an organism doubles in size, its number of cells also doubles, whereas its number of terminal units only increases by about 75% due to the 3/4 scaling law. Furthermore, the average distance between terminal units scales with body mass as a power law with exponent 1/12. To illustrate this, a blue whale is a hundred million times heavier than a shrew, but the average distance between its capillaries is only about 100,000,000^(1/12) ~ 4.6 times larger. This puts a constraint on the maximum size of mammals as their capillaries would not be able to supply enough oxygen to the increasing number of cells, which would in turn result in hypoxia of these cells, eventually causing them to die.
The reason why there are no smaller mammals than shrews has to do with the branching of vessels in the circulatory system. The aorta, our thickest vessel, branches into two thinner vessels, which themselves each branch into two thinner vessels, and so on until the terminal units are reached, where metabolic energy is supplied to individual cells. In the upper, pulsatile vessels, blood flow is dominated by the wave motion generated by the heart, analogously to the sinusoidal AC wave of an electric current. This is also the reason why you can feel your pulse in these vessels. Further down in the nonpulsatile domain, blood flow is dominated by the viscous drag forces. Here, the blood is no longer pulsating and flows very slowly down the vessels, just like water in a pipe (analogously to DC current). All mammals have about 15 branchings in the nonpulsatile (DC) domain; however, they differ in the number of branchings in the pulsatile (AC) domain. Humans have about seven or eight such branchings, a whale has 16–17, and a shrew just one or two. When decreasing animal size, a tipping point will be reached where the network can only support nonpulsatile DC flow. Such an animal would have a beating heart, but no pulse, and it would be a very inefficient design as non-pulsatory vessels need much more energy due to the viscous forces than pulsatory ones. Due to the parsimony and efficiency by which natural selection operates, no smaller mammal than the shrew has yet evolved.
Growth, Ageing and Death
Growth cannot happen without a perpetual supply of energy and resources. The energy budget of the growth process in which metabolic energy is supplied is allocated between new growth and maintenance and repair. In the beginning, almost everything goes into growth. Upon maturity, however, everything goes into repair, maintenance and replacement. To express this in the words of scaling, as an animal doubles in size, its number of cells and thus the amount of energy required for sustenance also doubles. However, metabolic rate only increases by a factor of 2^(3/4), or 1.682, rather than the required factor of 2. So the rate at which energy is needed for maintenance increases faster than the rate at which metabolic energy can be supplied, forcing the amount of energy available for growth to systematically decrease and eventually go to zero. It is this mismatch between the scaling of maintenance and supply that eventually results in the cessation of growth.
As far as ageing and death are concerned, all evidence seems to point toward "wear and tear" as the underlying origins. Similar to the flow of water through pipes or the flow of cars on highways, the flows in our biological networks also lead to wear and tear, eventually resulting in damage and decay. In organisms, this damage occurs at the cellular and intracellular levels, i.e. at the terminal units of networks where energy resources are exchanged (e.g. capillaries). It is primarily caused by two factors: 1) wear and tear of blood vessels due to viscous drag forces of the blood, and 2) chemical damage from free radicals, which are by-products from the production of ATP (the primary energy carrier of cells) in respiratory metabolism (i.e. oxidative damage to DNA). In other words, the very systems that sustain us are at the same time also damaging and degrading our bodies. However, within this principle lies the reason why larger animals live longer than smaller ones. Their metabolic rate is lower; at the cellular level they suffer systematically less damage at a slower rate, resulting in a correspondingly larger lifespan.
We know that metabolic rate increases exponentially with temperature and is also modulated by the amount of calories consumed. Therefore, life span can theoretically be extended by lowering body temperature and caloric intake, thus lowering metabolic rate and subsequent cellular damage. Indeed, there is evidence from studies on mice that halving caloric intake results in a 75% increase in lifespan. However, would you rather lead a cold, sedentary, calorically restricted, but extended life or an active, comfortable, regular life rich in activity and experience?
Network Principles & Origins of Scaling
The origins of scaling laws in biology are rooted in the universal mathematical, dynamical, and organizational properties of the multiple networks that distribute energy, materials, and information to local microscopic sites such as cells and mitochondria in organisms. West's work has distilled out three fundamental properties that transcend the tremendous diversity of biological (and, as it turns out, also non-biological) networks. These are:
1) Networks are space-filling. This means that the terminal units need to feed all cells in the body (or, for urban systems, supply each house with roads and utility networks such as gas, water, and electricity).
2) The terminal units are invariant. The capillaries of the circulatory system, mitochondria within cells, or petioles (the last branch) of plants and trees have the same size within each taxonomic group.
3) The system is optimized, meaning that the energy used is the smallest it could possibly be given its design and network constraints. This is the result of the continuous multiple feedback and fine-tuning mechanisms implicit in the ongoing processes of natural selection that have been playing out over enormous periods of time.
Remarkably, these network properties can also be found outside of biology, as we shall see in a moment.
The Fourth Dimension of Life
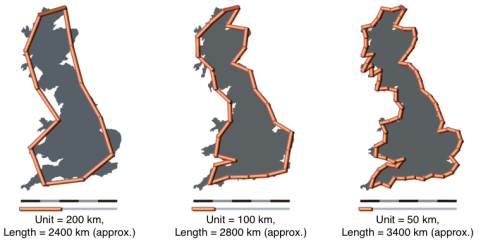
The geometric origin of the quarter-power scaling law derives its magic number 4 from our three-dimensional world in space plus one fractal dimension. This goes back to Lewis Richardson, who looked at data containing measurements of countries' borders and got different numbers from different datasets, reflecting the fact that these measurements were taken at different resolutions. The higher the resolution, the longer the border became, particularly if the border line was very crinkly, as lower resolutions would not capture the increased lengths resulting from that crinkliness (see figure below). This was then further developed by Benoit Mandelbrot, who took Richardson's analysis and formally introduced the fractal dimension based on the self-similarity of physical objects. Basically, the smoother the border line (e.g. South Africa), the lower its fractal dimension. The more crinkly the border, the higher its fractal dimension (e.g. Norway), i.e. the longer it becomes upon each increase in resolution. Even though it's a line of "ordinary" dimension 1, its crinkliness can cause it to behave as if it were an area in terms of scaling properties, therefore having a fractal dimension of 2. Similarly, if an area is crinkly enough, it can behave like a volume, with Euclidean dimension 2, but fractal dimension 3. This additional dimension, which in biology arises from maximizing exchange surfaces and thus optimizing performance, leads to organisms' functioning as if they are operating in four dimensions. If we lived in a 7-dimensional world, these power laws would be governed by multiples of 1/8, rather than 1/4.
Scaling of Cities and Social Networks
Similar to organisms, cities also underlie these fundamental power law scalings and follow the same space-filling network principles outlined above. These are roads, railways, electricity lines, etc. which have also evolved based on continuous feedback mechanisms inherent in a selective process toward an approximate optimization by minimizing costs and time. However, instead of the quarter-power exponents that govern organisms, the exponents 0.85 and 1.15 play a critical role in urban systems. Infrastructure, i.e. the lengths of roads and pipes, number of gas stations, etc. scales sublinearly with population size with exponent 0.85. In contrast, socioeconomic quantities such as number of patents, income, and the global domestic product (GDP) scale superlinearly with exponent 1.15. This is due to the increased interactions and social lives that people lead in big cities. However, the good is also matched by the bad and the ugly, meaning that crime and disease also scale with exponent 1.15. Thus, all you need is the size of a city within a particular national urban system and you can predict with 80–90% accuracy its average wage, number of patents produced, how long all of its roads are, how many AIDS cases it has had, how much crime was committed, how many restaurants there are, etc. These predictions don't hold true between national urban systems, as they depend on metrics such as overall economy, culture, and individuality and thus are unique to each nation.
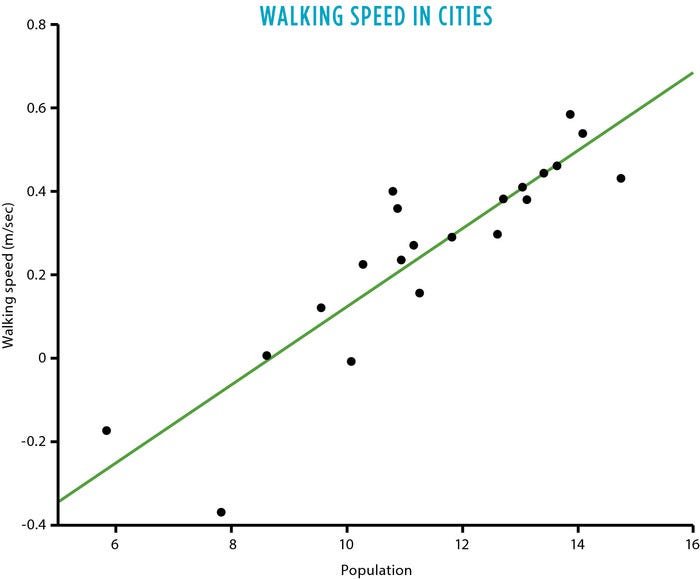
The scaling of urban systems is also highly correlated with the scaling of social networks. Averaged over time, each person interacts with a number of other people as well as with groups of people in the city in such a way that collectively their network of interactions fills the available 'socioeconomic space', conforming to the space-filling property of scaling laws. There is a natural explanation for why social connectivity and therefore socioeconomic quantities scale superlinearly with population size. Socioeconomic quantities are the sum of interactions or links between people and therefore depend on how correlated they are. However, there are limitations on the magnitude of how many people an individual can realistically interact with. The limitations in the number and rate of interactions we can sustain with other people in the city is rooted in the hidden constraints imposed by space and time. We simply can't be in all places at all times. Still, increased city size yields more social interactions per capita, which generates more socioeconomic wealth while simultaneously decreasing infrastructural needs. This in turn leads to another prominent feature of modern life: a continually speeding-up pace, which even manifests itself in trivial features such as walking speed (see figure below).
Furthermore, scaling laws provide insights into the remarkably regular structure of movement in cities. Given any particular place in a city, such as a downtown area or a shopping mall, it can be predicted how many people visit this very location from any distance away and how frequently they do it. More formally, the number of visitors scales with both the distance traveled and the frequency of visitation as a power law with exponent -2. To illustrate this, suppose that Park Street in Boston is visited on average by 1,600 people from 4 kilometers away once a month. Now, we can predict how many people visit from 8 kilometers away with the same frequency of once a month. Since the distance now increased by a factor 2, applying the power law with exponent -2 would yield 2^(–2) x 1,600 = 1/4 x 1,600 = 400 people. Similarly, 64 people (5^(–2) x 1,600) visit once a month from 20 kilometers away (i.e. five times as far). Likewise, these predictions can be made with changing frequency of visitation. Now, let's assume we want to know how many people visit Park Street from 4 kilometers away twice a month. This also obeys the same power law with exponent -2 and thus leads to a result of 400 people. Similarly, 64 people visit from 4 kilometers away five times a month. As we saw before, this is the same number as the people visiting once a month from five times as far away (20 kilometers). This is an example of a fascinating general symmetry of mobility: if the distance traveled multiplied by the frequency of visitation to any specific location is kept the same, then the number of people visiting also remains the same. In our case, 400 people visited Park Street both once a month from 20 kilometers away (1 x 20 = 20) and five times a month from 4 kilometers away (4 x 5 = 20). These kind of predictions can be a very powerful tool for planning and development as they provide a framework for estimating the flux of people to and from a specific area of the city. Such predictions can have a wide implication in urban development, including the building of a new mall or football stadium or the development of a housing project for instance.
Scaling of Companies
Studies on the Compustat dataset, which is provided by S&P 500 and consists of 28,853 companies that were traded on US markets between 1950 and 2009, show that the half-life of a company is roughly 10.5 years, meaning that 50% of companies die after only 10.5 years. Only very few make it over 100 years, with even fewer making it over 200 years. Out of all these companies, 22,469 (78%) had died by 2009. Others were acquired by or merged with other companies, some went bankrupt or were liquidated, others were privatized, underwent leveraged buyouts, or went through reverse acquisitions. Here, companies seem to have survived through diversification and innovation. When the number of companies is plotted logarithmically as a function of life span (figure not shown), exponential decay and a constant mortality rate can be revealed.
The longest surviving companies are relatively modest in size and are highly specialized, operating in niche markets such as ancient inns, wineries, breweries, confectioners, restaurants, and the like. These seem to have survived by continuing to produce a perceived high-quality product for a small, dedicated clientele. Interestingly, most of them are Japanese.
In order to achieve greater efficiency while striving for greater market share and increased profits, companies typically add more rules, regulations, and protocols, very often at the expense of R&D, which should be the major insurance policy for a company's long-term survival. Thus, while the dimensionality of cities continually expands, the ones of companies continually contracts, eventually stagnating. Market forces usually limit the initial excitement and enthusiasm for new products, which leads to only a few successful products as the company is trying to gain a foothold and an identity, creating economies of scale. Most become very unidimensional by focusing only on short-term goals. This reduction in diversity, along with the lack of R&D and other predicaments, are classic indicators of reduced resilience and are typically a recipe for eventual disaster. It is worth adding that unlike companies (or organisms for that matter), cities are remarkably resilient and don't seem to die at all, not even when great damage is done to them, such as Hiroshima, Nagasaki, or Detroit.
Accelerating Pace of Life
The Industrial Revolution was the socioeconomic equivalent of the Big Bang. In 1500, the world's population stood at only 500 million people. It took 300 years to double this number to 1 billion in 1800, another 120 years to double again to 2 billion in 1920, and only 45 years to double again to 4 billion in 1965. Thus until recently, the doubling time has been increasing superexponentially. We are on track to reach a possible 12 billion by the beginning of the next century.
The Anthropocene began roughly 10,000 years ago, when we started to significantly diverge from being predominantly biological to predominantly social by increasing our effective metabolic rate (from 90 watts to more than 3,000 watts). West suggests that with the advent of the Industrial Revolution, we have entered another era, which he calls the Urbanocene, characterized by the exponential rise of cities which now dominate the planet. He also warns about the finite number of resources available on our planet and points out that it would be prudent to switch from a closed system, where energy is being used from our planet, to an open system, where energy is harnessed from the sun. The total amount of energy delivered by the sun to the Earth is about 10¹⁸ kilowatt-hours a year, compared with our "measly" needs of 1.5 x 10¹⁴ kilowatt-hours. This only amounts to 0.015 percent of the total annual energy supplied by the sun. Therefore, we need technology that allows us to harness abundant energy from the sun, predominantly from direct radiation, but also indirectly from wind, tidal forces, and wave motion in order to build a sustainable environment.
Exponential growth is characterized by a continuously increasing function that eventually becomes infinitely large as it approaches an infinite time value. Therefore, since it theoretically takes infinitely long to get there, this growth is rendered harmless. However, superexponential growth, as we have been experiencing it, is faster than just exponential and thus clearly unsustainable as it requires an unlimited and ever-increasing amount of resources and energy at some finite time point in the future. This scenario will almost certainly result in eventual stagnation and collapse of the system, unless some groundbreaking, paradigm-shifting innovation is made that allows us to reset the clock by changing the conditions under which the system has been operating and growth has been occurring. Such paradigm-shifting innovations include the discovery of bronze, coal, and oil, the invention of information technology, the internet, and so on.
However, the time passing between these reset cycles is getting shorter and shorter. There were most likely thousands of years between the Stone, Bronze, and Iron Ages — all major paradigm shifts in human history. By contrast, it only took about two decades to move from the computer age to the information age. This pattern leads to the prediction that we are due for a major paradigm shift in the next 20–30 years. Overall, more innovations will be needed over shorter periods of time to continually reset the clock so the system can take off again, until another innovation will be needed. How many of those cycles can we go through? Can we keep up with the ever-increasing pace of life? As West proposes, we need a grand unified theory that allows to understand how the world works in a quantifiable and predictive framework, in order to ensure our continued survival.
West G., 2017, Scale. The universal laws of growth, innovation, sustainability, and the pace of life in organisms, cities, economies, and companies, New York, Penguin Press.
Source: https://medium.com/swlh/scale-a-book-summary-3d39d16321ef
0 Response to "Geoffrey West Scale Blue Whale 11000 Calories"
Post a Comment